Part V: Impact of 2020 limits

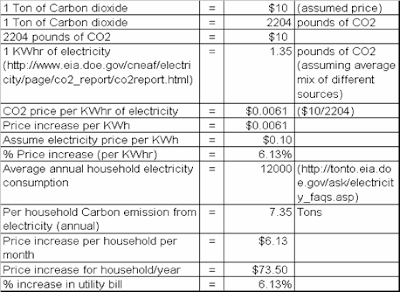
The previous posts showed the calculations for the revenue collected in the short-run (up to 2012), where the time frame is too short for the producers to change the means of production (no changes in the supply curve) and the consumers respond only to the price, but cannot alter their demand habits (i.e., no shift in the demand curve, just going up and down) . Over the longer time-frame, the consumer habits can certainly change, and the long-run elasticity has been estimated to be 0.7 for electricity. The emissions reduction is expected to be 17%. If we assumed that the producers are unable to change their production mix at all (not a realistic assumption, but this will provide the worst case, highest cost answer), then once again, the price of carbon can be estimated using the relationships described in part IV.

Interestingly, even though the limits for 2020 are ~6X the limit for 2012, the price increases from $24.5 to only $39.5, ~60%. The reason for this significantly lower increase is the higher value of elasticity of demand for electricity over the long run.

Part IV: Elasticity of Demand and the Price for CO2

In this section, the carbon price is evaluated using the elasticity of demand of electricity*. The elasticity of demand for electricity has been estimated to be ~0.2 in the short run, and ~0.7 in the long run. In subsequent calculations, the short-run value of 0.2 is assumed for calculations, providing a conservative estimate of the reduction in the emissions. In the short-run (2009-2012), it is unlikely that there will be significant deployment of any new technology for electricity generation, and therefore, the entire reduction in emissions has to occur through a reduction in consumption. The WM targets are a 3% reduction in the emissions, and therefore, we have:

DQ/Q (for electricity) = 0.03

Elasticity =0.2

--> DP/P (for electricity) =0.03/.2=0.15

Therefore, electricity is 15% more expensive due to WM. Since this 15% increase in electricity price is entirely due to the carbon price, the price of carbon may be estimated as:

DP/P=0.15 ==> DP = 0.15*P = 0.15*0.1 ($/KWhr)= $0.015 /KWhr

1KWhr = 1.35 pounds of CO2 = $0.015

1 Ton = 2204 pounds of CO2 = 2204*0.015/1.35 = $24.5/Tonne of CO2.

This value is clearly higher than the floor price used in earlier calculations ($10), indicating that the "fundamental value" of a CO2 permit is ~$25 in the period up to 2012. The estimates for periods beyond 2012 are fraught with uncertainty, because of the following reasons:

(1). Higher (and uncertain) elasticity of demand

(2). Possible role for deployment of new technologies (though 10 years seems relatively small from a utility context. However, other possibilities, such as plug-in hybrids could indeed be deployed faster, resulting in faster changes in demand).

Since the actual CO2 price is $25 per tonne, the price increase per household is now 24.5/10*73.5 ~ $180 per household per year.

*Elasticity of demand refers to the % change in demand of a good due to a specific % change in price. For details, see here.

Part III: Revenues from Cap and Trade (Floor Price = $10)

The revenues from cap and trade can be estimated in a straightforward manner by estimating the area of the shaded rectangle in the figure below.

The price increase per household is $73.5 per year, and there are 110M households in the country, leading to $8.5B/year. This calculation is for carbon emissions from electricity only. The total size of the carbon markets can be estimated as ~6B Tons of CO2 at $10 being ~$60B in the early stages.

Part II: Limits to CO2 Emission

Carbon dioxide emissions may be reduced by two means: (1). Limits (2). Taxes. The difference between the two approaches is whether we choose a vertical control or the horizontal control in the supply-demand diagram, and they both have their pros and cons.

Limits on CO2: Caps

Let us first consider limits (or "caps") on carbon emission. Intuition tells us that if the limit is higher than the amount currently emitted, then the CO2 price is zero, and there is no change in the amount of CO2. So, the first requirement is that the limit set should be less than the amount emitted. This might seem obvious, but could pose problems during early stages of implementation if the emitted amounts are not known with a high degree of confidence. In fact, this uncertainty wreaked havoc in the European Emissions Trading Scheme (EU ETS) , where prices collapsed after it was discovered that the caps were set too high.


Fig. 2. Price of energy vs. the quantity of CO2 emitted in the presence of a limit (Cap). In this case, the price of electricity = marginal cost + cost of CO2.

When the limits are set lower than the current levels of emission, then equilibrium requirements dictate that the price of electricity has to rise sufficiently such that the intersection of the demand curve with the limit is now the price of electricity. Since the cost of the electricity by itself (production cost) has not changed, the difference between the two horizontal lines is therefore the cost of CO2.

Now, cost estimation can be done given the limits and the demand curve. Since limits are not set yet, and the obtaining the demand curve is non-trivial, we have to resort to other means for estimation. We can use the range of prices observed in the European market as a guide to estimate. (Note that the CO2 price is completely determined by the limits being set and the demand curve, and therefore, the regulator can choose any value such that the price falls in a desired band.)

The calculations are given below, along with the assumptions and the sources of the data.


Therefore, under the simple assumptions that we listed above, the average house-hold is likely to spend $6.13 per month higher once the legislation is introduced. If the carbon price increases, the amount will also increase. The plot below shows the linear relationship (Additional amount spent = 0.613*Price per Ton of CO2) between the carbon price and the additional amount to be spent by the household.

Micro-economic Analysis of Waxman-Markey bill: Part 1: No Limits

I haven't seen an analysis of the provisions in the Waxman-Markey bill in terms of basic supply and demand. This post is also an attempt to make back-of-the-envelope calculations on how much the individual household has to pay additionally if Waxman-Markey is implemented. This post is a bit wonky, but should be accessible to a lay person. Any comments and suggestions are welcome.

Let us first consider the relatively simpler case of power generation. We first start with the assumption that the producers of electricity have a constant (marginal) cost (The implications of relaxing this assumption will be addressed in subsequent posts). For example, the (marginal) cost of electricity is ~$0.12/KWHr.

Fig. 1. Price vs. Quantity, assuming a constant marginal price for energy. The intersection of the two lines is the equilibrium price (same as the marginal price) and the equilibrium quantity, which is the quantity that will be consumed.

The demand curve (which is the curve representing the quantity demanded Q at any price P) is downward sloping, as the demand is likely to be high if energy is cheap. For example, people drive more (resulting in more demand for energy) when gas is cheap and less when it is more expensive.

Note: One could argue that nobody demands CO2, and therefore this whole argument is flawed. However, even though CO2 is a pollutant, which is a "bad" rather than a "good" that we actually want, supply-demand arguments are still applicable. This is because the CO2 is actually a byproduct of the good that we seek, which is energy.

In the absence of any limits the quantity of CO2 emitted is the equilibrium quantity, which happens to be 5.6 GigaTons in the US (~44,000 lbs of CO2/per person). In the next post, we will focus on limits and the basis for determination, taxation vs. cap and trade etc.

Preventing Windfalls to the Polluters

Here is a piece that argues that, even the Waxman-Markey bill has allocations to regulated utilities, it is able to preserve the carbon price, and therefore, the bill is appropriate. The key distinction appears to be that the permits are given to the distribution company rather than the generator.

Carbon Pricing and Avoided Deforestation

It is rare that there is positive news on the environment, but this economist article points out an actual case where the"financial innovation"may have actually helped save the rainforest. The carbon sequestration capability of the rainforest is pegged at 1Tonne per hectare, and the world wide acreage of the rainforest is quoted as being 1B Hectares. Therefore, the monetary value of the Carbon permits sold amounts to $10B worldwide. Now, the US timber industry alone has $30B in revenue, so, the question is: Is carbon pricing sufficient to ensure that forests are not destroyed? It appears that additional externalities due to forests (benefits such as habitats for animals and plants, and prevented losses, such as soil erosion) may need to be factored into calculations to ensure that the forests are not destroyed.